The images on this page were created when I was working on the paper
"Another Veech Triangle," which is available here.
You can construct a translation surface from unfolding the triangle with angles
Pi/12, Pi/3, and 7Pi/12. Alternatively, you can construct this surface by taking the regular 12-gon,
and gluing equilateral triangles to each of the edges, and then identifying the triples
of triangles that differ by a translation. The result is a surface of
genus 4 and admits (infinitely) many decompositions into parallel cylinders.
Some of these are pictured below:
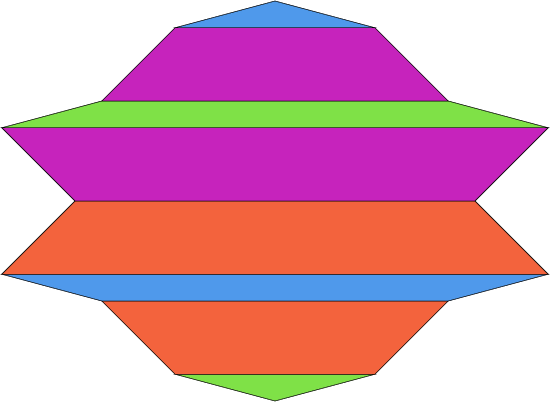
This is the first decomposition in the paper.
Available for download as
[
ps]
[
pdf]

This is the third decomposition in the paper.
Available for download as
[
ps]
[
pdf]

If w is e^(i*Pi/6) is the 12th root of unity, then the cylinders are parallel to the vector
3+3w-w^3 in the complex plane.
Available for download as
[
ps]
[
pdf]

If w is e^(i*Pi/6) is the 12th root of unity, then the cylinders are parallel to the vector
4+5w-2w^3 in the complex plane.
Available for download as
[
ps]
[
pdf]

If w is e^(i*Pi/6) is the 12th root of unity, then the cylinders are parallel to the vector
5+6w-2w^3 in the complex plane.
Available for download as
[
ps]
[
pdf]

If w is e^(i*Pi/6) is the 12th root of unity, then the cylinders are parallel to the vector
6+5w-2w^3 in the complex plane.
Available for download as
[
ps]
[
pdf]
I decided to share these pictures, because I find them aesthetically pleasing. If for some reason
you would like to create more you can take a look the software I used to make it: [tar.gz]
(Though, the code is probably not very readable)




