Duality in Projective Geometry

In Projective Geometry, there is a dual notion between points and lines in the plane. That is, the space of all lines in the projective plane, 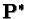\({\bf P^{\ast}}\) ,is a space satisfying all the axioms required of a projective plane. Moreover the two spaces are exactly equivalent, in that if the term ``line'' is exchanged with ``point'' and ``collinear'' with ``coincident'' and ``intersection'' with ``join'' etc. then there is no way to tell a difference between the geometry we started with and the geometry afterwards.

 

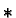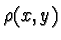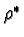Duality is usually denoted with an \(\ast\) used as a superscript. For example, we defined \(\rho(x,y)\) to be an operation on pairs of collinear triples of points in the plane,that maps each of these pairs to a line according to Pappus' Theorem. Thus we can define \(\rho^{\ast}\) to be its dual. Then 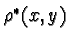\(\rho^{\ast}(x,y)\) is an operation on pairs of coincident triples of lines in the plane, that map each of these pairs to a point according to the dual to Pappus' theorem.

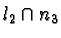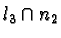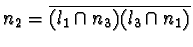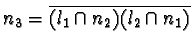Let l1, l2, and l3be three distinct coincident lines and m 1, m2,and m3 be three more distinct coincident lines incident at a different point. Then we define n 1 to be the unique line containing the two points \(l_{2} \cap n_{3}\) and \(l_{3} \cap n_{2}\) .Similarly we can define \(n_{2}=\overline{(l_{1} \cap n_{3}) (l_{3} \cap n_{1})}\) and \(n_{3}=\overline{(l_{1} \cap n_{2}) (l_{2} \cap n_{1})}\) .The dual to Pappus' Theorem states that these three lines are coincident. 

The applet below demonstrates the dual to Pappus' theorem.

alt="Your browser understands the <APPLET> tag but isn't running the applet, for some reason." Your browser is completely ignoring the <APPLET> tag!Get Netscape. 

You can move the blue and the green points which in turn move the blue or the green lines that these points are incident on. The red lines indicate the lines constructed by the dual to Pappus' theorem and the point represents 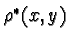\(\rho^{\ast}(x,y)\) .

Next Step: Observation Two