Construction of Fractal Curves

© 2012 by W. Patrick Hooper. Licensed under a Creative Commons Attribution 3.0 Unported License.

Purpose: We describe the method we use to construct these fractal curves. We will create the Java classes which carry out these constructions.

  1. Kock CurveKock Curve
    This image was created by Antònio Miguel de Campos is in the public domain.

    The construction of the Koch snowflake

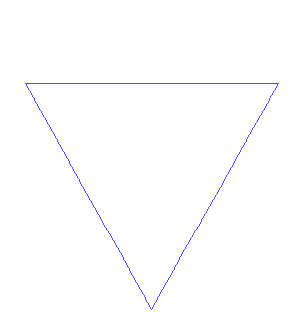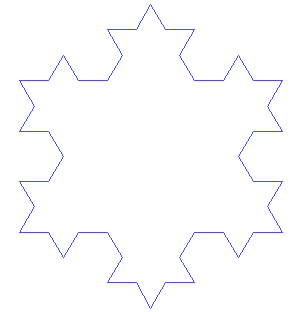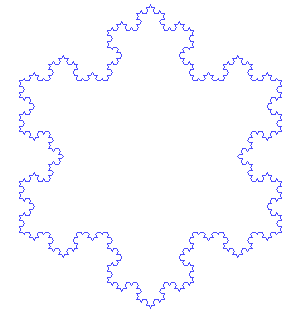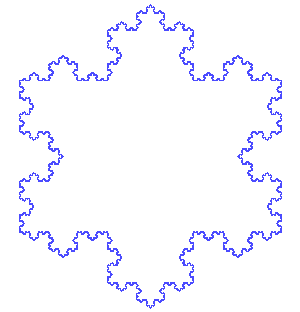
    The Koch snowflake is a closed curve which is the limit of a sequence of polygons, as suggested by the image at right.
    1. Our construction of the Koch snowflake has a few basic ingredients:
      1. An orientation preserving similarity of the complex plane, C, is a map T : C → C of the form T(z)=a z+b.
      2. A polygonal path in the complex plane, C is just a list of points (joined by line segments). For instance, we can represent the closed square as the list S=< 0, 1, 1+i, i, 0>.
      3. Similarities act on polygonal paths by acting on each of the individual points. For instance, if T(z)=iz+1, then
        T(S)=< T(0), T(1), T(1+i), T(i), T(0)>=< 1, i+1, i, 0, 1>.
      4. If two polygonal paths begin and end with the same point, then we can concatenate them with the ∗ operator. E.g.:
        < 0, 1, i > ∗ < i, 1+i, 2, 3 > = < 0, 1, i, 1+i, 2, 3 >.
    2. Path Substitution:
      1. Now suppose that γ is a polygonal path which begins at 0 and ends at 1. For instance, to construct the snowflake, we define
        γ = < A=0, B=1⁄3, C=(3+Sqrt(3)*i)/6, D=2⁄3, E=1 >.
        This path is shown below.
        The curve γ
      2. Let P=< p0, p1, p2, …, pn> be an arbitrary polygonal path. For each k=0, … n-1 we define Tk to be the orientation preserving similarity so that Tk(0)=pk and Tk(1)=pk+1.
      3. The substitution operation Sγ on polygonal paths is given by
        Sγ(P)=T0(γ)∗T1(γ)∗ … ∗ Tn-1(γ).
    3. Our construction:
      1. Let γ = < A=0, B=1⁄3, C=(3+Sqrt(3)*i)/6, D=2⁄3, E=1 >. as above.
      2. Let P0 be a closed equilateral triangle oriented clockwise such as
        P0=< 0, 1, (1-sqrt(3)*i)/2, 0>.
      3. Our approximates of the snowflake are given by inductively defining Pi+1=Sγ(Pi) for i≥ 0.

    4. Mathematics of the Koch snowflake

      Of course, what was described above is not new. Here are some references:
      1. One third of the Koch snowflake is an set which is invariant under an iterated function system.
      2. It is a theorem of Hutchinson that an iterated function system satisfying a certain contraction property has a unique invariant compact set. See "Fractals and self similarity."
      3. A good introductory text on the subject is "Measure, topology, and fractal geometry" by Gerald Edgar.

  2. LineSegment:

    Our program will have a few classes and interfaces to work with certain geometric objects. These will be in a our geometry package. The first class in this package is a class to work with line segments. The following class defines a line segment in the plane. 
    public final class LineSegment {
    private final Complex start, end;

    public LineSegment(Complex starting_point, Complex ending_point) {
        start = starting_point;
        end = ending_point;
    }

    public Complex startingPoint() {
        return start;
    }

    public Complex endingPoint() {
        return end;
    }
}
    The class also includes a method to compute the length of a line segment, and a method to return the midpoint. See the full source code here: LineSegment.java.

  3. Planar Maps and an introduction to interfaces:

    Our program will have a few classes and interfaces to work with certain geometric objects. These will be in a our geometry package.

    An interface is a collection of prototypes of methods without implementations. The advantage of creating interfaces is that it allows us create multiple implementations which can be used interchangeably.

    Planar Maps: We will define an interface called PlanarMap, it will contain the prototype for a single function which describes the map of the plane. The following code defines this interface:

    package geometry;

import number.Complex;

public interface PlanarMap {
    Complex map(Complex z);
}

    Above, the map function above is a prototype of a method which takes as input a complex number and outputs a new complex number.

    What follows are two implementations and a demonstration program:

    1. Similarity: The Similarity class gives an example implementation of the PlanarMap interface. The following class represents an orientation preserving similarity of the plane. (An orientation preserving similarity of the Complex plane is a map of the form z maps to w*z+a.) 
      package geometry;

import number.Complex;

public final class Similarity implements PlanarMap {
    private final Complex w,a;
    
    public Similarity(Complex w, Complex a) {
        this.w=w;
        this.a=a;
    }   

    /** Apply the similarity to z returning w*z+a. */
    public Complex map(Complex z) {
        return w.mult(z).add(a);
    }
}
      The words implements PlanarMap indicates that the Similarity class will include all the methods in the PlanarMap interface. This is just the map function.
    2. Complex Polynomial: This class represents a complex polynomial, which can of course be thought of as a map of the plane. It is probably worth looking at the source code here: ComplexPolynomial.java.
    3. PlanarMapDemo: This class demonstrates how a single method can used with any implementation of a PlanarMap. 
      public class PlanarMapDemo {
    /** Apply the map f one hundred times to the point z and return the result. */
    public static Complex applyOneHundredTimes(PlanarMap f, Complex z) {
        for (int i = 0; i < 100; i++) {
            z = f.map(z);
        }
        return z;
    }
    
    public static void main(String[] args) {
        Complex z=new Complex(0.5, 0.8);

	/** The following defines the map z maps to 3*i*z/4+1. */
        Similarity f=new Similarity(new Complex(0,0.75),new Complex(1));
        System.out.println("We have f^100(z)="+applyOneHundredTimes(f,z)+".");

	/** The following defines the map z maps to z^2. */
        ComplexPolynomial g=new ComplexPolynomial(new Complex(0), new Complex(0), new Complex(1));
        System.out.println("We have g^100(z)="+applyOneHundredTimes(g,z)+".");
    }
}
      See the full source code here: PlanarMapDemo.java.

  4. The path package

    We will create another package for working with paths.
    1. What is a path? We might define a path in the complex plane to be a continuous map γ:[0,1] → C.
      We can approximate such a path by polygonal paths:
      • P0 = <γ(0), γ(1)>
      • P1 = <γ(0), γ(1⁄2), γ(1)>
      • P2 = <γ(0), γ(1⁄4), γ(1⁄2), γ(3⁄4), γ(1)>…
      • Pn = <γ(0⁄2n), γ(1⁄2n), γ(2⁄2n), …, γ(2n⁄2n)>…
      It follows from uniform continuity of γ that (with the obvious parameterizations) these polygonal paths converge uniformly to γ.

      We might call the process of moving from Pn to Pn+1 refinement. In general, a refinement replaces each edge with a polygonal path which better approximates the desired curve.

      From this point of view, the edges of a path play a more fundamental role than the vertices. We will take this into account when creating our definition of path.

    2. Java's Iterator class An iterator is a very useful interface built into java. Here is the interface java.util.Iterator: 
      package java.util;

public interface Iterator<E> {
	boolean hasNext();
	E next();
	void remove();
}
      Some comments:
      1. This is a generic interface, meaning that the E in Iterator<E> indicates some arbitrary type (a class or interface) which is specified when creating an iterator. For purposes of a implementing a polygonal path, E might be LineSegment.
      2. You can think of an iterator as an object which moves through an ordered collection of objects (such as edges of a polygonal path).
      3. The interface has three methods. The hasNext() method checks if the iterator has another object of type E to return. The next() method returns the next object. The remove() method removes the last object returned from the Collection. The remove() is often not implemented. See the API documentation for more information.
    3. EdgeIterator We will use much the same idea to build an iterator over edges. Our code for the EdgeIterator interface follows: 
      package path;

import geometry.LineSegment;

public interface EdgeIterator {

    boolean hasNext();

    LineSegment next();
}

      We can use objects of this type just as we use Java's Iterator type. We will use it to iterate over the edges of a polygonal path.

    4. The interface PolygonalPath.
      Here are some goals for our definition of this interface:
      1. A polygonal path has a beginning and end.
      2. You should be able to iterate over the edges in the path, so it should be able to return an iterator which moves over the edges making up the polygonal path.
      These requirements are accomplished by the following interface definition: 
      package path;

import number.Complex;

public interface PolygonalPath {

    Complex startingPoint();

    Complex endingPoint();

    EdgeIterator iterator();
}

    5. The class VertexPath:

      The simplest type of path would be just a polygonal path constructed from a specific list of vertices.
      1. Java has a built in definition of a List interface as well as various implementations we can use (such as ArrayList and LinkedList). The beginning of our implementation is: 
        import java.util.*;         // For working with lists.
import number.Complex;

public class VertexPath implements PolygonalPath {
    
    private final List<Complex> vert;    // The list of vertices
    
    /** Construct from a list of complex numbers. */
    public VertexPath(Complex... vertices) {
        // Vertices is an array of complex numbers.
         vert=new LinkedList<Complex>();
        for (int i=0; i<vertices.length; i++) {
            vert.add(vertices[i]);
        }
    }
}

        The list vert stores our vertices. The type of the list is List<Complex>. The <Complex> indicates that this will be a list of Complex numbers. The List interface is a generic interface meaning that the list can store any specified type of object. Java has many built in classes for working with common data structures involving collections of objects, including lists.

        This constructor is called with a list of Complex numbers. So we can build a triangle with:

         VertexPath p = new VertexPath( new Complex(0.0),new Complex(1.0),
 	new Complex(0.5, -Math.sqrt(3) / 2), new Complex(0.0) );

        Inside the constructor, we make vert a new linked list of Complex numbers. Here, the parameter vertices is an array. We iterate from i=0 to i = (vertices.length-1), and add each vertices[i] to our vertex list.

      2. The start and end points: We must return the starting and ending point of the path. 
        public Complex endingPoint() {
  return vert.get(vert.size() - 1);
}

public Complex startingPoint() {
	return vert.get(0);
}
        The code just returns the first and last compex number in the list vert.
      3. Returning an edge iterator: We must be able to return an iterator over the edges. Such an iterator must have access to vert, which stores our vertex data. It must also be able to store some data, namely a current location in the vertex list. The best way to do this is with an inner class, a class inside the VertexPath class. Here is the code: 
         private class MyEdgeIterator implements EdgeIterator {

     private Iterator<Complex> vertex_iterator;
     private Complex current_vertex;

     public MyEdgeIterator() {
         vertex_iterator = vert.iterator(); // Create an iterator which moves over the vertices.
         current_vertex = vertex_iterator.next(); // Record the first vertex.
         // The next vertex returned by "vertex_iterator.next()" will be the 2nd vertex of the list.
     }

     /** Return true if there is another segment in the path. */
     public boolean hasNext() {
         return vertex_iterator.hasNext(); // return true if vertex_iterator has another vertex.
     }

     /** Return the next segment in the path. */
     public LineSegment next() {
         Complex a = current_vertex;
         current_vertex = vertex_iterator.next();
         return new LineSegment(a, current_vertex);
     }
 }

 /** Return an iterator over the segments making up the path. */
 public EdgeIterator iterator() {
     return new MyEdgeIterator();
 }
        We emphasize that the above code all appears inside the VertexPath class. Further comments:
        • The inner class MyEdgeIterator is private so it can only be accessed directly from inside the VertexPath class.
        • The inner class can access our vertex list, vert.
        • The iterator() method creates and returns a new MyEdgeIterator, which is a special type of EdgeIterator. The calling code can use all the methods in the EdgeIterator interface.
        The above showed just part of the file VertexPath.java.

    6. Paths and PathIterators

      Our idea of a Path is very close to our idea of a PolygonalPath. 
      public interface Path {

    Complex startingPoint();

    Complex endingPoint();

    PathIterator iterator();
}


      public interface PathIterator {

    boolean hasNext();

    Path next();
}

      Observe that a Path is define very much like a PolygonalPath. The only difference is that instead of allowing the program to iterate over line segments, it allows the program to iterate over paths.

    7. The UnitCircleExample class:

      This class gives an example implementation of the Path interface. The class represents the unit circle in the plane. These are the interesting bits: 
      public class UnitCircleExample implements Path {

    private VertexPath path;
    
    public UnitCircleExample() {
        // Begin with a polygonal approximation using the fourth roots of unity.
        path = new VertexPath(new Complex(1, 0), new Complex(0, 1), new Complex(-1, 0),
                new Complex(0, -1), new Complex(1, 0));
    }

    /** Takes a segment with endpoints on the unit circle, and returns a path
     *  constructed from three points on the circle. */
    private UnitCircleExample(LineSegment s) {
        Complex m = s.midpoint();
        path = new VertexPath(s.startingPoint(),
                m.div(m.abs()), // midpoint projected onto circle
                s.endingPoint());
    }

    public Complex startingPoint() {
        return path.startingPoint();
    }

    public Complex endingPoint() {
        return path.endingPoint();
    }

    private class CircleIterator implements PathIterator {

        EdgeIterator it;

        public CircleIterator() {
            it = path.iterator();
        }

        @Override
        public boolean hasNext() {
            return it.hasNext();
        }

        @Override
        public UnitCircleExample next() {
            // it.next() returns the next segment in the path. 
            return new UnitCircleExample(it.next());
        }
    }

    public PathIterator iterator() {
        return new CircleIterator();
    }
}
      You can view the full source code here: UnitCircleExample.java. The code includes a main method which demonstrates the class.

    8. The SubstitutionFractal class:

      Recall our fractal construction involved iteratively replacing all edges in a path p with the image of a fixed polygonal path gamma under the similarity sending the endpoints of γ to the endpoints of the edge. Here the source code excluding most comments and some boring parts: 
      public class SubstitutionFractal implements Path {

    final PolygonalPath p;
    final PolygonalPath gamma;
    
    public SubstitutionFractal(PolygonalPath p, PolygonalPath gamma) {
        this.p=p;
        this.gamma=gamma;
    }

    private class SubstitutionIterator implements PathIterator {
        private EdgeIterator it;
        
        public SubstitutionIterator() {
            it=p.iterator();
        }

        public boolean hasNext() {
            return it.hasNext();
        }

        public SubstitutionFractal next() {
            Similarity sim=new Similarity(it.next()); 
            // sim is the similarity sending 0 and 1 to the endpoints of the segment it.next().
            
            // "new VertexPath(gamma,sim)" gives the image of gamma under the similarity.
            return new SubstitutionFractal(new VertexPath(gamma, sim),gamma);
        }
    }

    public PathIterator iterator() {
        return new SubstitutionIterator();
    }
}
      You can view the full source code here: SubstitutionFractal.java.

    9. Additional Classes

      1. The PolygonalApproximation class: This class allows the user to access the nth polygonal approximation to a path directly (as a PolygonalPath). You can view the full source code here: PolygonalApproximation.java.
      2. The KochSnowflakeExample class: This demonstrates the use of the SubstitutionFractal class to represent the Koch Snowflake. You can view the full source code here: KochSnowflakeExample.java.

Useful Links

Valid XHTML 1.0 Strict Valid CSS!

This presentation is part of a Mathematical Research Oriented Java Tutorial, which aims to introduce students to the benefits that writing computer programs can provide to their understanding of mathematics.