A Complex Class in Java

Purpose: Learn about classes which can be instantiated as an object through the example of complex numbers.

Create a Complex Numbers Project.

By now you have some experience creating a Java project following the HelloWorld tutorial. Follow the directions below to create new project.
1. Select New Project.
2. Select "Java" from categories and "Java Application" from projects. Then click next.
3. Set Project Name to "ComplexProject." Choose a Project Location and Project Folder.
4. Choose "ComplexDemo" for the main class. Click finish.
5. The project should be created, and the file "ComplexDemo.java" should open.
Create a "number" package and a Complex class inside

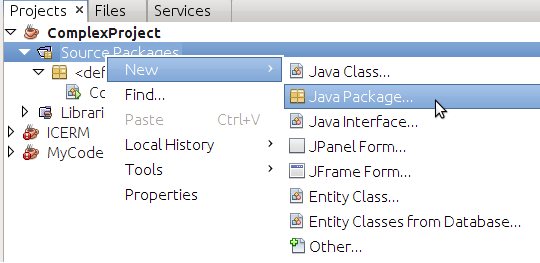
A package is just a collection of java classes. It is stored on the computer as a folder or directory.
1. To create a package named "number", switch to the Projects tab in the left pane. Then right click on "Source Packages" and select "New > Java Package" from the menu that appears. See the image at right.
2. Enter "number" for the Package Name and click "Finish".
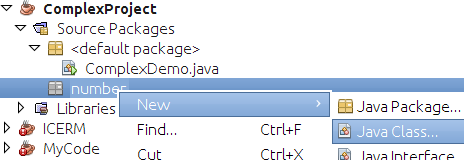
3. A new package named "number" should appear in the Project Tab. Right click on the package and select "New > Java Class" as below. For a class name select "Complex". Click finish, then Complex.java should open.
The Complex Class.

A complex number consists of a real and imaginary part. We will create a class which stores this data (the fields of the class).
1. Immutable: We will follow a convention that our complex numbers will be immutable. That is, once a complex number is created it can't be changed. This is good for calculations for instance. It is nice to guarantee that a number won't change in the midst of a calculation. The first step in realizing this is to insert the word "final" between "public" and "class" in the class definition. Now you should have the line:
```
public final class Complex {
```
2. The stored data: We will store the real and imaginary parts as a doubles. To do this we add a line to the Complex class in Complex.java, so the file reads:
```
public final class Complex {
    final private double x, y;
}
```
  This line indicates that a Complex number will contain two variables x and y each of which stores a double value (the real and imaginary parts, respectively).
  
  There are two modifiers in this statement. The word "private" means that we will only be able to access these variables (directly) from functions within this class. The word "final" means that once the values of x and y are set, they are permanent. This contributes toward the goal of making the class immutable.

Constructors.

Typically a java object is created using a constructor.

We will create two constructors. They appear as follows:

public final class Complex {
    final private double x, y;

    public Complex(double real_part, double imaginary_part) {
        x = real_part;
        y = imaginary_part;
    }

    public Complex(double real_part) {
        x = real_part;
        y = 0;
    }
}

The first constructor takes as input two doubles, and sets the variables x and y using this input.

The second constructor produces a real number from just one input.

Static creation
A java object can also be created from the class using a static method. For instance:
```
public static Complex fromPolar(double r, double theta) {
    return new Complex(r*Math.cos(theta), r*Math.sin(theta));
}
```
Because of the static keyword, the method can be called by referring directly to the class. For instance, we can construct a 7th root of unity with the line:
```
Complex z = Complex.fromPolar(1,2*Math.PI/7);
```
Methods for working with complex numbers.

The following are some of the methods from the Complex class.
1. The following code returns the real part of a complex number:
```
public double re(){
    return x;
}
```
  The absence of the static keyword means that this method can only be called from a Complex object. For instance, the following is a reasonable way to to use this method:
```
Complex z = Complex.fromPolar(1,2*Math.PI/7);
System.out.println("The number "+z.re()+" is the real part of a 7th root of unity.");
```
2. The square of the absolute value of a complex number:
```
public double absSquared() {
    return x*x+y*y;
}
```
3. The absolute value of a complex number:
```
public double abs() {
    return Math.sqrt(absSquared());
}
```
  Note that this code calls our absSquared method and then uses a static method from java.lang.Math to compute the square root. (A static method can be called just using the class name, while most methods such as our method re() require an object to call them.)
4. The following method returns the complex conjugate:
```
public double conj(){
    return new Complex(x,-y);
}
```
  Note that this method calls one of our constructors.
5. Return the sum of this complex numer and another:
```
public Complex add(Complex z) {
    return new Complex(x+z.x, y+z.y);
}
```
6. The multiplicative inverse of a complex number:
```
public Complex inv() {
    double abs_squared=absSquared();
    return new Complex(x/abs_squared, -y/abs_squared);
}
```
You can also view these functions in the Complex.java file. The source code in Complex.java is well commented. If you have questions, these comments might help to answer them.
Methods for interfacing with the Java language.

Every class extends the java.lang.Object class. This means that you can call all the methods from the Object class on any object that appears in Java. (This includes pretty much everything, except arrays and primitive types such as int and double.)
1. toString.
  The simplest method in java.lang.Object is the toString method, which converts the object to a string. By default, the toString method prints some useless information. We will override (replace the default implementation) with a more suitable version shown below:
```
public String toString() {
    if (y==0) {
        return ""+x;
    }
    if (y>0) {
        return ""+x+"+"+y+"*I";
    }
    return ""+x+"-"+(-y)+"*I";
}
```
  To understand this code, recall that adding to a string has the effect of concatenation. So the line return ""+x;, returns the string formed by concatenating the empty string "" and x. Here, x is converted to a string using whatever Java's standard format for doubles is in Java.
  
  We taylor what we return to the particular complex number. So we convert only the real part if the imaginary part is zero. Otherwise we print both parts. We also carefully consider the sign in front of the imaginary part.
  
  You can also do much more fancy number formatting with java, but there is no need to worry about this until you need to. See the links at the end of this page.
2. The equals method:
  Java uses the equals method to decide if two objects are equal. The method must return true if the complex number is equal to another object, and false if not.
  In particular, we need to be able to compare a complex number with any object in Java. This makes the code of this method more complex, fortunately, NetBeans has a shortcut for overriding this method, which generates the following code:
```
public boolean equals(Object obj) {
    if (obj == null) {
        return false;
    }
    if (!(obj instanceof Complex)) {
        return false;
    }
    Complex other = (Complex) obj;
    if (x != other.x) {
        return false;
    }
    if (y != other.y) {
        return false;
    }
    return true;
}
```
  Here is a detailed explanation of what this function is doing:
  1. The equals method is passed a Java Object. The first if statement checks to make sure it is not null. A variable is null before it is initialized, for instance. If it is null, we exit the method by returning false. (Note that double equals, ==, tests for equality while single equals indicates an assignment of value.)
  2. The second if ensures that obj is a complex number. If the object passes this test, then we know that obj is a complex number in disguise. So we convert the object to a complex number which we name other. (The exclamation point indicates logical negation, so the if statement can be read "If obj is not an instance of the Complex class, then return false.")
  3. The remainder of the code checks the real and imaginary parts to see if they match. It returns true if they match and false otherwise. (The != for inequality. So if (x != other.x) can be interpreted as "if the real part of this complex number and the real part of the other complex number differ, then...".)
  As mentioned above, NetBeans has the ability to write an equals method for you. To achieve this, be sure your class does not have an equals method.
  - Right click somewhere in the text of the class and outside the text of a function. A menu will pop up. Select "Insert Code" as below.
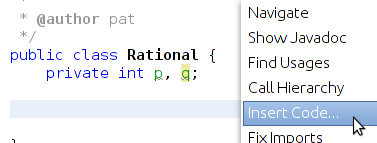
  - Then select equals and hascode as below.
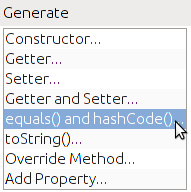
  - A window should pop up asking which fields you would like to include in the methods. Typically, all fields are used. (You should always use the same set of fields for both the equals and hashcode.) Then click "Generate" to produce the methods.
  Slightly technical remark: The hashcode() function returns an int. The implementation of this function is supposed to guarantee that whenever to objects are equal, they return the same hashcode. This is useful for quickly assembling a collection of distinct objects. See the documentation for HashSet and HashMap for instance.

The ComplexDemo class.

We will create a ComplexDemo class to demonstrate how to use our Complex class.

This class should have been created when you created the project. The source is below:

import number.Complex; // Allow us to use our complex class

public class ComplexDemo {
    public static void main(String[] args) {
        Complex a=new Complex(1.41235123,2.3145432), b=new Complex(3,4);

        System.out.println("I created two complex numbers: a="+a+" and b="+b+".");

        System.out.println("The absolute values of these numbers are |a|="+a.abs()+
            " and |b|="+b.abs()+".");
        System.out.println("The sum of these numbers is a+b="+a.add(b)+".");
        System.out.println("The difference between these numbers is a-b="+a.minus(b)+".");
        System.out.println("The product of these numbers is a*b="+a.mult(b)+".");
        System.out.println("The ratio of these numbers is a/b="+a.div(b)+".");
        System.out.println("A sanity check: (b/a)*a-b="+b.div(a).mult(a).minus(b) +".");

	Complex z = Complex.fromPolar(1,2*Math.PI/7);
        System.out.println("A primitive 7th root of unity is "+z+".");
    }
}

To run the program select "Run > Run Main Project" using the NetBeans menus.

Useful Links:

Relevant parts of the Oracle's Java Tutorial:
- Learning the Java Language: A more in depth look at some of the things touched on briefly here.
- A tutorial on working with numbers in Java: Discusses primitive types such as int and double, as well and the use of java.lang.Math.
- Discussion of immutable objects.
- Tutorial on working with Strings: This tutorial describes the basics for working with strings.
  You can also do more complex number formatting. See the Number formatting part of the tutorial.
Other examples
- Andrew G. Bennett has a Complex Function grapher built using java. He uses a more elaborate Complex.java.
- An example Rational.java and BigRational.java from Introduction to Programming in Java by Robert Sedgewick and Kevin Wayne

This presentation is part of a Mathematical Research Oriented Java Tutorial, which aims to introduce students to the benefits that writing computer programs can provide to their understanding of mathematics.

A Complex Class in Java

Create a Complex Numbers Project.

Create a "number" package and a Complex class inside

The Complex Class.

Constructors.

Static creation

Methods for working with complex numbers.

Methods for interfacing with the Java language.

toString.

The equals method:

The ComplexDemo class.

Useful Links: