An Alternate Model for Langton's Ant:

Recall that the ant only has two options when he reaches a square: turn left or right. Then he must leave the square. We can combine this knowledge with our knowledge that the grid must be checkered to create an alternate model for the Ant's movements:

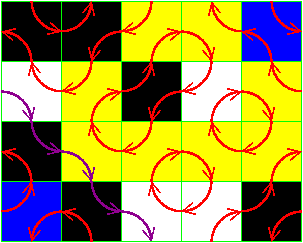
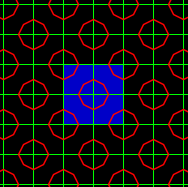
From the picture at right, it becomes obvious that the at each quadrilateral of the grid, the ant can only come in two of the sides and leave one of the two others (turning left or right). Its a question of holonomy, the ant moves around in some path, and when he returns he is facing one of two directions.


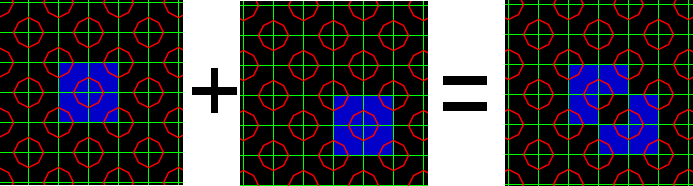
We replace a tile similar to:
 
with one of:
Replace this:
 [0]: turn left
Black
 [1]:turn left
Blue
 [2]:turn right
White
 [3]:turn right
Yellow
With this:




The tiles increment exactly as before, here we use the color red, to indicate that the tile will change the next time the Ant visits the square, and black to indicate that the ant must return twice before the tile changes. White tiles would be replaced similarly (ie: look at the arrows not the checkering). Our starting position would then be "circles around every other vertex of our grid."

One advantage of this model is that it makes the proof of symmetry and returning to the origin infinitely often easier to prove. Here is the idea:
  1. At any point in time our grid is covered by an infinite family of closed paths, all but finitely many are circles around vertices.
  2. There is a property we will call the Good Painter Property (GPP) which we will state later.
  3. Our argument is inductive. The grid starts as a symmetric grid with the GPP.
  4. Clearly any closed path in our grid can intersect each square at most twice.
  5. If our grid has the GPP, then any path on the grid intersects each red square at most once.
  6. Thus when our Ant moves around a path in a grid with the GPP, it must return to the place it started (ie. its trajectory is exactly the path it lies on). (What could go wrong? The only thing that could wrong is the Ant visits a red square and then revisits it along the same path, thus being redirected along a different path)
  7. If our grid is symmetric with the GPP and our Ant is positioned along the axis of symmetry, the path our Ant will take will be symmetric and thus when the ant returns to its original position again the grid will regain its symmetry.
  8. We must show that if the GPP holds for our grid, the GPP holds after the Ant moves all the way around a path in our grid. Then the result will follow.
The fairy tale version of our argument is: The Ant is a good painter. He starts with a good and symmetric canvas. Then he paints layer upon layer of paint on his canvas never violating the rules he learned which make him a good painter. His painting is good and symmetric, and he continues to paint his painting making it better and better and living happily ever after.

The Good Painter Property:

So what is the Good Painter Property?
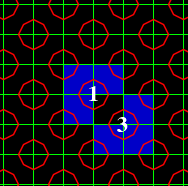
The idea is that the "red" tiles, tiles of type [1] and [3], occur in groups. You'll notice that the first time the Ant returns to the origin (after making 4 left turns), the grid looks like this:

This is the simplest group. The second simplest group consists of 6 squares (shown here for type [3], yellow squares):
 or 
Either white or black squares can appear inside. Notice that in all these cases, the paths intersect yellow/blue squares exactly once (this is the content of 5 above).

Vertices inherit a "checkering" from the drawing above as well based on whether the closest arrows wind clockwise or counter-clockwise around the vertex. The center of the blue square in this picture corresponds to counter clockwise (the Ant turns left on blue squares).


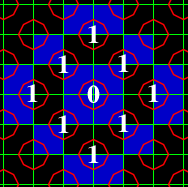
The idea is for squares of types [1] and [3] we can "add" 2-by-2 squares of the same type which have the right orientation relative to the vertex they surround. Our "addition" is modulo 2, so that

The condition that our grid has the Good Painter Property (GPP) is that there is as a finite sum of properly oriented 2-by-2 squares of type [1] which give us exactly all the type [1] squares in our grid, and similarly there is as a finite sum of properly oriented 2-by-2 squares of type [3] which give us exactly all the type [3] squares in our grid. The GPP makes no restriction on the occurance of type [0] or type [2] squares.


Now, given a grid with the GPP there are many different ways to write a sum. Namely, two occurances of the same 2-by-2 square will cancel. So one cannonical way to write a sum would be to require that each 2-by-2 square occurs in the sum at most once. But this is not the cannonical sum we will look at. We will require that our sum have the following form:
  1. The number of occurances of a 2-by-2 square in the sum must be equal, one less, or one more than adjacent 2-by-2 squares (adjacent in the sense that their centers are located diagonally across a square from one another)
  2. For all integers n, let Sn be the set of all 2-by-2 squares that occur more than n times in the sum. We require that any loop in the adjacency graph of 2-by-2 squares contained in Sn has in its interior only elements of Sn (a kind of simply connected retriction on the level sets)
Condition 1 outlaws sums of the form: (numbers indicate the number of occurances of the 2-by-2 square surrounding them)


Condition 2 outlaws more complicated pictures: (think of it as a mountain, as you move toward the center you must step up never down into a valley)
Not
But


It is clear that such a redefinition of the sum is possible. Start with the canonical sum, if property (2) does not hold for some loop in Sn, add 2 copies of each relevant interior 2-by-2 square until it does hold. This can be done in such a way that property (1) remains true. This can be repeated inductively until you obtain the desired sum.

Now the boundary of each Sn forms an impenetrable fortress that the curves do not pass through. That is curves on the interior stay on the interior and curves on the exterior stay in the exterior. Moreover, it can be seen that every blue (or yellow) square must lie on the boundary of some Sn. This shows (5) of our proof above, that curves in the a grid with the GPP intersect each square of type [1] or [3] at most once.

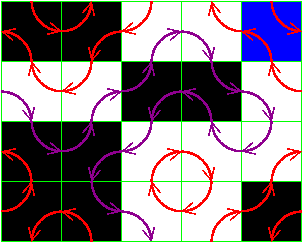
Below shows a group of blue squares with the GPP and the "barrier" seperating the  inside and the outside in purple.


Proof of GPP persistence (and symmetry, returning of Ant):

It remains to show that the GPP persists through one complete loop.

The GPP turns out to be a natural property related to "always turning" paths in a square grid. Consider a closed path in a square grid  which can be written as a sequence  of right and left turns. We also require that the path never overlap itself (but we do allow the path to enter a square twice provided it neither enters nor leaves in the same direction twice).

Then color the places where the curve turns once to the left with our blue squares and the places that the curve turns once right with yellow squares (ignore squares visited twice):

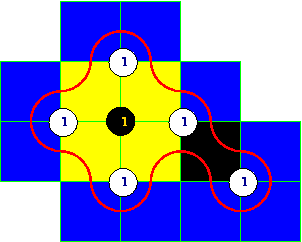
The yellow and the blue squares satisfy the GPP. We can get the blue colored squares as a sum of all the possible blue 2-by-2 squares with centers that lie on the interior of our curve. Similarly we get the yellow squares. The proof is simple. Our curve is a Jordan curve seperating the plane into two regions, thus on when it crosses a particular blue square once exactly one of the vertices on the diagonal transverse to the curve is on the interior. Consequently, there is only one blue 2-by-2 square that is taken in our sum that contains this particular square. Conversely if the curve hits a particular square either twice or never, both relevant vertices must lie on the same side of the curve, thus our sum of 2-by-2 squares cancels over or does not contain this particular square. Similar for yellow squares.

This gives us the simplest case of GPP persisting through a loop. Start with an all [0] (black) grid, then sprinkle finitely many [2] (white) squares randomly on the plane. This grid satifies the GPP because there are no squares of type [1] or [3].  Now consider a closed path in this grid, it looks like one we just described. After the Ant travels the path, he modifies the grid exactly as we colored it above. Consequently, this new grid also satisfies the GPP.

More generally if the grid satisfies the GPP, and the closed curve that the Ant travels contains no squares of type [1] or [3], then after he modifies the grid it also satisfies the GPP.

Next, we must deal with the possiblility that the curve may intersect squares of type [1] and [3]. This argument is somewhat more subtle. Recall that our curve cannot pass through the barriers seperating the interiors and the exteriors of groups of squares of types [1] and [3].  Recall also that each square of type [1] or [3] is contained in the boundary of some Sn.The idea is to reduce to the case we just proved by modifying the grid in some acceptable manner, changing the curve to path admisable in this new grid, leading the Ant along this new path, and then doing another acceptable modification that returns the grid back into what the ant would have done anyway.  Then we argue that the presistence of the GPP is obvious when looked at this way.

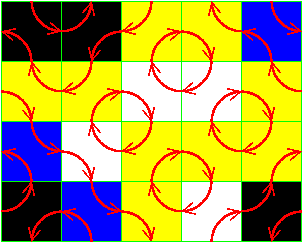
Lets do a simple example. Consider the purple curve in the picture below (part of a greater closed curve not shown). It bumps the yellow  ([3]- right turns) group shown, and may concievably as we continue outside the shown region return and bump the group yet again.

 We modify the grid so that
  1. We modify the square in the group first bumped +1 (mod 4). In this case the square first bumped of type [3] (yellow) becomes type [0] black.
  2. The values of all the squares in the boundary of the clump are decreased by 1 (mod 4). In this case changing squares of type [3] (yellow) into squares of type [2] (white).
  3. We turn all the squares in the interior of the group to the group's color +1 (mod 4). So in this case the two squares in the middle become both black.
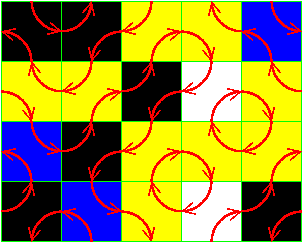
After modifying the grid in this way for each group bumped, we get a new purple path which never crosses squares of type [1] or [3]:

Next we let the Ant modify this new path obtaining this grid, which must satisfy the GPP by the argument before:


In the last step we replace the square where the group was first hit and return the squares in what used to be the interior of the region to there original types. Above the square first hit has become white (type [2]) and we replace it by +2 (mod 4) to become black (type [0]). We obtain this grid:

This is what the ant would have constructed had we not modified the grid at all. The interior of the clump satisfied the GPP, and besides this, we only replaces a square of type [2] with a square of type [0], thus the GPP is satisfied in the whole resulting grid.

This argument shows the GPP persists through the ant moving around a loop. There aren't to many modifications needed to show that this argument works for general loops in a grid with the GPP. If you believe this, we've proven that the ant returns to the square at which he starts infinitely often and at these points the grid is symmetric.

This argument must be modified to suit deformed grids.

HOME >>>>> VISUALIZATIONS >>>>> LANGTON'S ANT >>>>> GRID DEFORMAION