Basic Mathematics in Python

This notebook explains how to manipulate numbers in Python. It also gives examples of the while loop, if statements, and function definitions.

Types of numbers

Python supports both integer and floating point numbers. (A floating point number is a decimal approximation to a number.)

In [1]: 
3
Out[1]:
3
In [2]: 
-2
Out[2]:
-2
In [3]: 
3.14159
Out[3]:
3.14159

You can distinguish them with the type command. (But mostly, you should not need to.)

In [4]: 
type(3)
Out[4]:
int
In [5]: 
type(3.14159)
Out[5]:
float

Numerical Operations

Addition, Subtraction and multiplication behave more or less as you would expect. Note that floating point arithmetic is not exact because numbers are stored in binary and with limited precision.

In [6]: 
3+5
Out[6]:
8
In [7]: 
3.2-2.6
Out[7]:
0.6000000000000001
In [8]: 
1.1*2.2
Out[8]:
2.4200000000000004

Division always returns a floating point number.

In [9]: 
6/2
Out[9]:
3.0

For integer division, you can use //. The quotient a//b returns the greatest integer less than or equal to the fraction \(\frac{a}{b}\).

In [10]: 
6//2
Out[10]:
3
In [11]: 
7//2
Out[11]:
3
In [12]: 
-1//2
Out[12]:
-1

The remainder of the division is given by a%b. Assuming \(b>0\), this always returns an integer \(r\) with \(0 \leq r \leq b-1\) and satisfying r=a-b*(a//b).

In [13]: 
12%3
Out[13]:
0
In [14]: 
13%3
Out[14]:
1
In [15]: 
-13%3
Out[15]:
2

You can compute powers with **.

In [16]: 
2**3
Out[16]:
8
In [17]: 
1.1**100.1
Out[17]:
13912.583514610875

You can use paretheses to control the order in which an expression is evaluated. The order of operations is the same as for mathematics. (Details on the order are in the Python Language reference.)

The following computes an approximation to the mathematical number \(e\).

In [18]: 
(1+1/1000)**1000
Out[18]:
2.7169239322355936

Storing values

You can store a value into a variable with the = operator. The following computes the area of the 3-4-5 right triangle:

In [19]: 
width=3
height=4
width*height/2
Out[19]:
6.0

Note that the value of a variable can change over time. This is quite useful in programming.

In [20]: 
x=0
x=x+1
print("The value of x is now",x)

The value of x is now 1

The print() command used above is quite useful. It can be used to print a list of strings (quoted text) and variable values. For example:

In [21]: 
print("The area of a triangle with width",width,"and height", height,"is",width*height/2,".")

The area of a triangle with width 3 and height 4 is 6.0 .

The print() function is described in §: 3.3 of The Python Standard Library.

Boolean values

Python also has objects True and False which are useful for logic.

In [22]: 
True
Out[22]:
True
In [23]: 
False
Out[23]:
False

Numerical Comparisons

You can use == to test for equality and != to test for inequality.

In [24]: 
2+3==5
Out[24]:
True
In [25]: 
2-5==3
Out[25]:
False
In [26]: 
2+3!=5
Out[26]:
False

You can also test for less than <, less than or equal to <=, greater than > and greater than or equal to >=.

In [27]: 
2<3
Out[27]:
True
In [28]: 
5<=2
Out[28]:
False
In [29]: 
x=2.2
x**2 > 9
Out[29]:
False

Table of Numerical Operations and Comparisons

This is a list of the basic numerical operations built into Python:

x+y addition
x-y subtraction
-x negation
x*y multiplication
x/y division: returns \(\frac{x}{y}\).
x//y floored division: returns \(\lfloor \frac{x}{y} \rfloor\), where \(\lfloor \cdot \rfloor\) denotes the floor function, i.e., the greatest integer less than or equal to \(\cdot\).
x%y remainder of division. Assuming \(y\) is a positive number, it returns a number \(z\) satisfying \(0\leq z \leq y\) and \(\frac{x}{y}=\lfloor \frac{x}{y} \rfloor+\frac{z}{y}\).
x**y exponentiation: returns \(x^y\).
pow(x,y) exponentiation: returns \(x^y\) same as x**y
abs(x) absolute value

The following table lists the available comparisons:

x==y test for equality: returns true if the numbers are equal and false if not.
x!=y not equal: returns true if the numbers are unequal and false if they are equal.
x<y returns true if \(x\) is less than \(y\).
x>y returns true if \(x\) is greater than \(y\).
x<=y returns true if \(x\) is less than or equal to \(y\).
x>=y returns true if \(x\) is greater than or equal to \(y\).

Flow control

The while statement

A while loop executes as long as the following statement is true. The following prints the numbers 1...10.

In [30]: 
i=1
while i<=10:
    print(i)
    i=i+1

1
2
3
4
5
6
7
8
9
10

Note that a colon : was required at the end of the while statement. The two statements underneath were indented with four spaces. Only the indented statements are repeated, as the following example computing 10! illustrates.

In [31]: 
i = 1
factorial = 1
while i<=10:
    factorial = factorial*i
    i = i+1
print(factorial)

3628800

The if statement

An if statement executes an indented block of code if a statement is true.

In [32]: 
a = 5
b = 12
c = 13
if a**2 + b**2 == c**2:
    print("This is a Pythagorean triple.")

This is a Pythagorean triple.

You can also add an else block to do something if the statement is false.

In [33]: 
n=13
if n%2==0:
    print("The number n =",n,"is even.")
else:
    print("The number n =",n,"is odd.")

The number n = 13 is odd.

The term elif is short for "else if". The block under elif is executed if the statement in the above if clause is false and the statement after elif is true.

In [34]: 
mets = 5
yankees = 3
if mets > yankees:
    print("The Mets win.")
elif mets < yankees:
    print("The Yankees win.")
else:
    print("The game was a tie.")

The Mets win.

You can have multiple elif statements and the else statement at the end is optional. At most one statement will execute (and necessarily one if there is an else clause).

In [35]: 
x=3.3
if x<1:
    print ("The number x is less than one.")
elif x<2:
    print("The number x is in the interval [1,2)")
elif x<3:
    print("The number x is in the interval [2,3)")
elif x<4:
    print("The number x is in the interval [3,4)")

The number x is in the interval [3,4)

Functions

In Python, a function is a block of code which evaluates depending on some input variables. The code may do something and often returns a value.

Some simple functions emulate mathematical functions. For example, the function \(f(x)=x^2+1\) can be written and evaluated as follows:

In [36]: 
def f(x):
    return x**2+1
print("f(2) is ",f(2),".")
print("f(-3) is ",f(-3),".")

f(2) is  5 .
f(-3) is  10 .

The function is evaluated until it reaches the end of the block or a return statement as above. A return statement tells the function what it evaluates to.

You can have multiple return statements. The following illustrates the function \[g(x)=\begin{cases} x^2 & \text{if $x \geq 0$} \\ -x^2 & \text{otherwise}.\end{cases}\]

In [37]: 
def g(x):
    if x>=0:
        return x**2
    else:
        return -x**2
print("g(2) is ",g(2),".")
print("g(-2) is ",g(-2),".")

g(2) is  4 .
g(-2) is  -4 .

The following computes n factorial.

In [38]: 
def factorial(n):
    i = 1
    factorial = 1
    while i<=n:
        factorial = factorial*i
        i = i+1
    return factorial

print("5! is", factorial(5) )

5! is 120

You can pass multiple parameters to a function.

Functions can also return a truth value:

In [39]: 
def is_even(n):
    return n%2 == 0
print("The statement `5 is even' is", is_even(5) )

The statement `5 is even' is False

Other math functions

The math module contains more mathematical functions and constants. To use these methods you should import math first. This makes functions from math callable.

In [40]: 
import math
print("The number pi is", math.pi)

The number pi is 3.141592653589793
In [41]: 
print("The sine of 60 degrees is",math.sin(math.pi/3))

The sine of 60 degrees is 0.8660254037844386

The floor and ceil functions convert from floats to integers.

In [42]: 
print( "The floor of pi is", math.floor(math.pi) )
print( "The ceiling of pi is", math.ceil(math.pi) )

The floor of pi is 3
The ceiling of pi is 4

More functions are available. See the description of the math module in the Python Standard Library reference.

Passing functions to functions

Functions can be passed to functions which allows them to solve more general problems. The following function secant_slope will take as input a real valued function \(f:{\mathbb R} \to {\mathbb R}\) and two input values \(x_1\) and \(x_2\) and produce the slope of the associated secant line (the line joining \(\big(x_1, f(x_1)\big)\) to \(\big(x_1, f(x_1)\big)\)).

In [43]: 
def secant_slope(f, x1, x2):
    return ( f(x1)-f(x2) )/(x1- x2)

Here are two examples. First we compute the secant line of \(f(x)=x^2\) through the points on the graph with \(x_1=0\) and \(x_2=1\).

In [44]: 
def square(x):
    return x**2
print("The slope of the secant line is", secant_slope(square, 0, 1))

The slope of the secant line is 1.0

Now we will compute the secant line of \(f(x)=\cos(x)\) through the points on the graph with \(x_1=0\) and \(x_2=\frac{\pi}{4}\). Note that we don't need to write our own cosine function; we use the math library loaded above.

In [45]: 
print("The slope of the secant line is", secant_slope(math.cos, 0, math.pi/4))

The slope of the secant line is -0.37292322857805654

Examples

Example 1.

The following function computes the area of a triangle from its three side lengths. This is the semiperimeter formula for area of a triangle.

In [46]: 
import math
def area(a,b,c):
    s=(a+b+c)/2
    return math.sqrt(s*(s-a)*(s-b)*(s-c))
In [47]: 
print("The area of the the 3-4-5 right triangle is", area(3,4,5))
print("The area of the equilateral triangle with side length one is", area(1,1,1))

The area of the the 3-4-5 right triangle is 6.0
The area of the equilateral triangle with side length one is 0.4330127018922193

Example 2.

The Collatz conjecture asserts that the following function terminates for any integer \(n \geq 1\). This conjecture is still unresolved.

In [48]: 
def collatz(n):
    while n!=1:
        if n%2==0:        # if n is even
            n = n//2              # divide n by 2
        else:
            n = 3*n+1     # otherwise when n is odd: multiply by three and add one.
        print(n)

We'll test this on the value 101.

In [49]: 
collatz(101)

304
152
76
38
19
58
29
88
44
22
11
34
17
52
26
13
40
20
10
5
16
8
4
2
1

Example 3.

An approximation to a definite integral of a real valued function is \[\int_a^b f(x)~dx \approx \frac{b-a}{n} \sum_{i=0}^{n-1} f\Big(a+\frac{i(b-a)}{n}\Big)\] for large values of \(n\). Here is a function which evaluates this sum on an arbitrary function.

In [50]: 
def approximate_integral(f, a, b, n):
    step_size = (b-a)/n
    i=0
    sum=0
    while (i<n):
        sum = sum + f(a+i*(b-a)/n)
        i=i+1
    return sum * (b-a) / n

To test this, we approximate the integral \(\int_0^1 x^2~dx\):

In [51]: 
def square(x):
    return x**2

print("The integral of x^2 over the interval [0,1] is approximately", approximate_integral(square, 0, 1, 100))

The integral of x^2 over the interval [0,1] is approximately 0.32835000000000003

We also approximate \(\int_0^\pi \sin(x)~dx\):

In [52]: 
print("The integral of sin(x) over the interval [0,pi] is approximately", approximate_integral(math.sin, 0, math.pi, 100))

The integral of sin(x) over the interval [0,pi] is approximately 1.9998355038874436

Exercises

  1. Write a function evalf(x,y) which takes two numbers \(x\) and \(y\) and returns the value of the expression \(f(x,y)=\frac{3xy+1}{x^2+1}\).
  2. Write a function quadratic_maximum(b,c) which takes two numbers b and c and returns the maximal value of the function \(f(x) = c + bx − x^2\).
  3. Suppose \(p\) and \(n \neq 0\) are integers. We call \(n\) a divisor of \(p\) if \(\frac{p}{n}\) is an integer (or equivalently if \(n\) divides \(p\) with zero remainder). Write a function print_divisors(p) which takes as input an integer \(p \geq 1\) and prints all its positive divisors.
  4. An integer \(p \geq 2\) is prime if the only positive divisors of \(p\) are itself and one. Write a function is_prime(p) which takes as input an integer \(p \geq 2\) and returns True if \(p\) is prime and False if \(p\) is not prime.
    Hint: The number \(p\) is not prime if and only if there is an integer \(n\) with \(2 \leq n < p\) so that the remainder when dividing \(p\) by \(n\) is zero.
  5. Write a function called is_square(n) which takes as input a integer \(n\) and returns truth-value of the statement "There is an integer \(k\) so that \(n=k^2\)."
  6. Write a function called sum_of_cubes(n) which takes as input a positive integer \(n\) and returns the sum \[1^3+2^3+3^3+\ldots+n^3=\sum_{j=1}^n j^3.\]
  7. Newton's method is a very efficient way to find a root of a differentiable function \(f\) starting with a point near the root. The method gives a sequence \(x_0, x_1, x_2, \ldots\) of numbers which rapidly approach the root if the initial point is sufficiently close to the root. The value \(x_0\) is the starting point. Given \(x_k\) the value of \(x_{k+1}\) by intersecting the \(x\)-axis with tangent line to the graph of \(f\) at the point \(\big(x_k, f(x_k)\big)\). That is, \[x_{k+1}=x_k - \frac{f(x_k)}{f'(x_k)}.\] An illustration of this process is shown at the end of this question.

    Write a function newtons_method(f,df,x0,n) which takes as input a function \(f:{\mathbb R} \to {\mathbb R}\), its derivative \(df=f'\) (also a function from \({\mathbb R}\) to \({\mathbb R}\)), an initial point \(x_0\) and an integer \(n \geq 1\). The function should return the value \(x_n\) obtained by iterating Newton's method \(n\) times.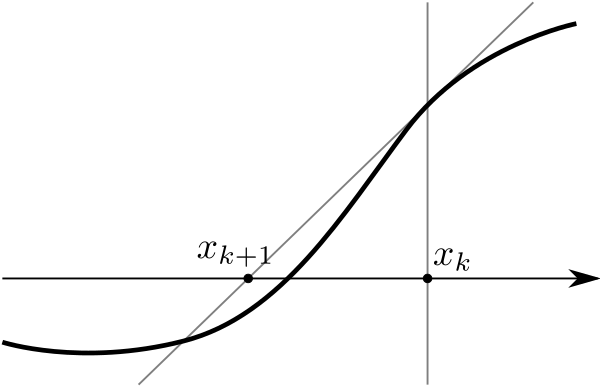

References